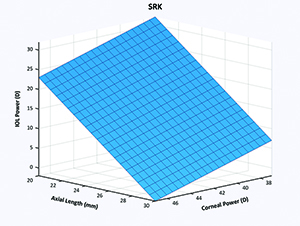
 |
| Figure 1. The original SRK formula is plotted as a plane in three dimensions. (Click to enlarge.) |
In our residency, we were first taught about the SRK formula for selecting intraocular lens power. It was the only one written in the American Academy of Ophthalmology monograph on cataracts. The formula is: IOL Power = A constant - 0.9K - 2.5 AL. We were also taught that there were more sophisticated formulas such as the Hoffer Q and the Holladay formulas. They existed and were good, but perhaps too sophisticated to comprehend. That was the end of our formal training and we went on to our careers. Throughout the next 20 years we, as many do, attempted to keep up with these and new formulas.
Over the next 10 years we came to a few conclusions. First, there was no one perfect formula for all situations. Second, although the formulas were similar in some ways, they were very different in subtle ways that could not be explained in simple terms. Also, it was very difficult to compare formulas in an objective way. And finally, optimization of any formula was critical to its accuracy.
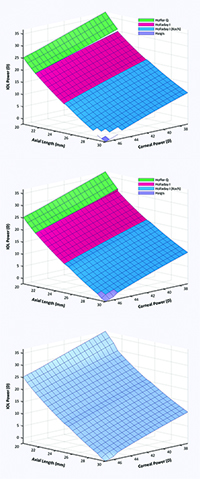 |
| Figure 2. The initial Ladas Super Surface was constructed using the strengths of four formulas: the Hoffer Q, the Holladay 1, the Holladay 1 with the Wang-Koch axial length adjustment, and the Haigis. Figure 2a. Sections of each formula based on axial length. Figure 2b. Formulas are connected. Figure 2c. Formulas are amalgamated into one Super Surface. (Click to enlarge.) |
Two Variables
We were always very interested in the formulas and what made each one better for specific subsets of eyes (short or long axial lengths, shallow anterior chambers, flat or steep k’s, etc.). They all had unique ways to determine the effective lens position, but they were all very different.
At some point, we realized that all of these formulas were essentially two-variable equations with corneal power and axial length on the x and y axis, respectively. The newer-generation formulas just added theoretical constants to make the formula more complex or adjusted it for other variables. We also started thinking about different ways to think about the math involved in these computations.
James Gleck, the author of Chaos, the 1980s book on entropy, stated very eloquently what we started to believe: “… graphic images are the key. It’s masochism for a mathematician to do without pictures … [Otherwise] how can they see the relationship between that motion and this? How can they develop intuition?”
So, with that mind-set we thought that, perhaps, one could go about developing a better formula than the many that existed. The first step was to graphically characterize an IOL formula. In its most simplistic form, the methodology can be demonstrated with the SRK formula in three dimensions.
This was the starting point: no longer thinking of these mathematical solutions as just numbers but as three-dimensional solutions to complex problems.
As we stated before, it is accepted that certain formulas work better in specific situations. This was a recurring conclusion that is hard to dispute. Many ophthalmologists have published tables of multiple formula choices that one could use in certain situations.
The pioneers of IOL calculation dealt with all these situations and described the dilemma in different ways throughout the years. For instance, the original SRK formula was updated with adjustment factors to shape it into the SRK II by altering the A-constant at different axial lengths. Dr. Ken Hoffer, as he advanced his formulas, placed parameters on the calculation of anterior chamber depth in his formula. Dr. Jack Holladay has described nine different eye anatomies to account for differences based on the axial length and the AC size, and added various additional input data to fine-tune his formula.
While these were great advances, it seems more likely that IOL calculations and the measurements that go into them are not a series of “if this, then that” statements, but rather a continuum.
Super Formula
This is where the derivation of a “super surface” and “super formula” comes into play. As previously mentioned, the newer-generation formulas featured theoretical constants that added subtle curves to the surface. Our original article demonstrated them in 3D.
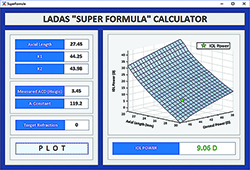 |
| Figure 3. For the IOL calculation in an eye with axial myopia, the Ladas Super Formula localizes to the portion of the Ladas Super Surface that automatically applies the Wang-Koch axial length modification and gives us an IOL power which proved to be spot-on with a postop refraction of plano. Calculated on-line at iolcalc.com. (Click to enlarge.) |
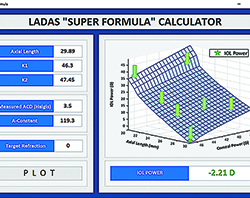 |
| Figure 4. Each part of the graph, some of which are shown with the green arrows, will be optimized and further honed in order to produce more accurate results. (Click to enlarge.) |
The utility of using the “super formula” can be shown in this everyday example of a lens calculation, shown in Figure 3. From the available options, the formula that you would choose for this scenario would be limited, first, by your access to them.
Then you would probably start to run through your understanding and knowledge about this particular set of input data. There have been articles that have concluded that the SRK/T may be better in longer eyes, or perhaps the Haigis. The Holladay I or Holladay II may be suitable in this situation. This was usually when one starts to look at the recommended IOL for his patient with multiple formulas until he realizes that the answers are different.
Another thing: Did you even consider adding the Koch adjustment to the Holladay I and relying on that? Do you remember the adjustment calculation? Based on peer-reviewed literature, that is the formula/adjustment that is incorporated into the “super formula” and your calculation will be based on that current state-of-the-art data. An IOL power of 9 diopters, as can be seen in Figure 3, was localized to the correct region of the surface in this individual eye.
Hopefully, this scenario solved a clinical dilemma in this particular case, but the “super formula” as it stands works with all eyes. It factors in appropriate formulas, adjustments to these formulas and lens design to select an appropriate IOL power for any eye.
Evolution of the Super Formula
If you conclude that this “super formula” is static and just an amalgamation of a few formulas, you’re mistaken, and you may be missing the point. The other conclusion that most would agree on is that optimization of a formula is the key to improving its accuracy. There are a few important points about optimization that are known to be critical. Thomas Olsen, the inventor of the Olsen formula, has emphasized these. First, optimization is formula-specific. Second, other variables such as ACD can be used to “optimize” a formula, such as was used in his paper on second eyes.2
The ability to optimize multiple formulas was not possible until now. The next step, which is currently under way and will continue, is evolution and enhancement of the super formula. Using our methodology, we can start to optimize each region of the surface. Thus, as is shown in Figure 4, we can go block-by-block and inch-by-inch on the surface and optimize it for a group of surgeons or individuals. We have recruited at least 10 major cataract and refractive groups to supply outcome data to us. With the help of Aazim Siddiqui, we have developed a program that analyzes outcome data and adjusts the surface. The Super Surface is dynamic and constantly evolving, with each adjustment helping to hone the IOL calculations further.
Another dilemma that we believe is solved by our methodology is this: Previously, anytime you optimized a formula or added a variable such as ACD, the entire “surface” was treated the same. This is problematic because the axial length and keratometry are intimately related to the calculation of the effective lens position and ultimate improvement of any formula.
 |
| Figure 5. The intuitive Ladas-Siddiqui graph can compare two different formulas and show the areas where there is clinical agreement (green) and clinical dilemma (red). Further studies and data should be focused in these areas of clinical dilemma. (Click to enlarge.) |
Comparing Formulas
Finally, using a comparative graph called the Ladas-Siddiqui graph (See Figure 5) we can compare multiple formulas and their results to determine where they differ. Rather than having to examine thousands of eyes to come to statistically significant conclusions on a better formula for a particular eye, we can target only those areas where there is a clinically significant difference. Thus, obtaining and analyzing the that data will save time and resources to improve the overall understanding and accuracy of formulas. Furthermore, future formulas and the effect of input parameters on the surface can be analyzed more precisely. For instance, we can target a specific region to examine the IOL calculations in a small subset of eyes. Some ophthalmologists have made the observation that ACD less than 2.6 makes the calculations more difficult and highly variable. We can examine only those eyes and perhaps adjust the formula with a measured variable such as ACD, white-to-white, or just optimize for that group in that specific region of the surface.
The concept of a “super surface” is a novel method to represent IOL calculation formulas in three-dimensions, and it can be used to help determine the ideal lens power for an individual eye. Not only does the “super formula” solve a problem as it currently stands, but it also becomes the blueprint or framework to further advances in the field of lens calculations. As more data is collected, that information will be incorporated into the Ladas Super Surface, which will evolve and improve over time. For more information, visit iolcalc.com. REVIEW
Dr. Ladas and Dr. Devgan have an ownership interest in the Ladas Super Formula and Ladas Super Surface and associated methodologies and processes. Dr. Ladas is in private practice as surgeon/director at Maryland Eye Consultants and Surgeons, 2101 Medical Park Dr., Suite 101, Silver Spring, MD 20902. Tel 301-681-6600, jladas@marylandeye.com. He is also an assistant professor of ophthalmology at Wilmer Eye Institute, Baltimore.
Dr. Devgan is in private practice at Devgan Eye Surgery, 11600 Wilshire Blvd, Suite 200, Los Angeles, CA 90025, 1 (800) 337-1969, devgan@gmail.com, www.DevganEye.com. He is also chief of ophthalmology at Olive View UCLA Medical Center and a clinical professor of ophthalmology at the Jules Stein Eye Institute, UCLA School of Medicine.
1. Ladas J, Siddiqui A, Devgan U, Jun A. A 3-D “Super Surface” Combining Modern Intraocular Lens Formulas to Generate a “Super Formula” and Maximize Accuracy. JAMA Ophthalmol. Published online October 15, 2015. doi:10.1001/jamaophthalmol.2015.3832
2. Olsen T. Use of fellow eye data in the calculation of intraocular lens power for the second eye. Ophthalmology 2011;118(9):1710-5. doi: 10.1016/j.ophtha.2011.04.030. Epub 2011 Jul 2.